Conceptualizing and other Generative Acts

Copenhagen, Denmark
Swing@mail.tele.dk

a) Introduction. Simple notions, concepts, and measurements

Consciousness cannot be separated from what consciousness is about, whether sensations, feelings, or mediations in the sense of “thoughts” or aesthetic creations. These mediations include music, dance, art, and–especially in our own Western culture–language, linguistic structures consisting of words and numbers. First, we shall here be concerned with the representation of a quite everyday notion about the experience of temperature.

Even concerning this linguistically and numerically mediated content of consciousness we recognize that representations may have different forms. Besides simpler “notions” about temperature as such we may also have genuine “concepts” (in the strict sense of the word) about it. But how are we to develop such concepts (or other more specific forms of representation)? That is, how are we to define the meanings of the words (and/or other representational moments) when talking about these things so as to include also numbers and their denominations? Furthermore, being able to do all this consequently also requires us to define further more abstract concepts such as, for instance, “identity.”

The question to be touched on here shall involve only a few such “intellectual” concepts developed outside of their real contexts that alone give them meanings; so, for example, we shall examine how the real concept of temperature is founded. In this connection we shall refer to a psycho-physiological theory about consciousness as such, the “motor theory” of consciousness, as proposed by Rodney Cotterill in his book Enchanted Looms (1998). He views consciousness to be in steady correspondence with–in addition, of course, to the functions of the brain and sense organs–the bodily functions of, among other things, the spindle system in the muscles. But let me affirm at the outset that this concept may in no way be viewed as a mere psycho-physiological phenomenon.

As a starting point I choose a common-sense technical example, the function of a thermostat. We adjust its pointer to 25° C and see what happens. The heating element switches on and the temperature increases until a control mechanism switches the electrical current off, not letting the temperature become too high; then the temperature falls and the control mechanism switches the heater on again not letting the temperature become too low. Then again the temperature increases a little, falls a little, and so on. Cf. figure 1 (left side).

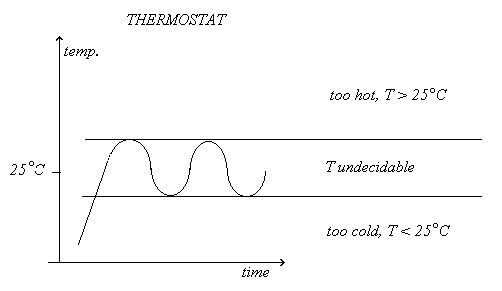
Figure 1

This diagram indicates three temperature domains (to the right). The upper domain indicates temperatures being “too high”; the lower one the temperatures being “too low.” In the first domain, the temperatures are certainly higher than the desired 25° C, in the other they are certainly below 25° C (“certainly” here in the sense of “undeniably”). The interesting domain, however, is rather the middle one indicating temperatures neither “too high” nor “too low.” But really, what is the temperature there? We don’t know–at least not exactly! We can only say that the temperature is appropriate, but that the exact temperature T in this middle domain is, indeed, undecidable.

2

Observe here the negations: “neither too hot nor too cold,” or “not too hot” & “not too cold.” Even the word “too” represents something as being not-convenient. Also observe–in this specific context–the use here of the positive negations. Thus “too hot” is not merely the negation of “too cold” but its positive contra-affirmation. And so also is ‘not too hot’ the positive negation, or contrapositive (in the sense of contra-affirmation) of ‘not too cold’ where the “not” in this connection is interpreted as simple negation.

We shall use this diagram reading in one further quite trivial way. We turn it around, letting its vertical temperature axis become horizontal like a kind of surface. Imagine this to represent a living space, for instance a long box in which to some hypothetical animals like ants or caterpillars one end is “too hot” and the other is “too cold.” These animals will therefore concentrate themselves in an area “neither too hot nor too cold,” “not too hot” & “not too cold.” We recognize, however, that these negations are merely linguistic expressions; language is the only medium in which we can express such negations explicitly. So our hypothetical animals will in no way be able to express themselves in this way, but they are nevertheless able to “express” themselves by tacitly (without mediation) realizing a local distribution somewhere in the middle of this box–and so “expressing” themselves through actual behavior–analogous to that of the thermostat. See figure 2.

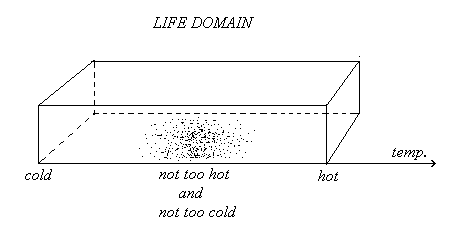
Figure 2

Here the part of the box indicated by the words “neither too hot nor too cold,” or “nottoo hot” & “not too cold” represents the milieu that makes life comfortable or at least possible to these animals. Accepting that “too hot” (call it h) in this connection is just the positive negation (the contra-affirmation, C) of “too cold” (c) we may write h = Cc. Further we here write the simple negation “not” as N and so “not too cold” as Nc, its opposition “not too cold” (using the double negation) as Nh = NCc. In this way we characterize the vital domain by means of the complex expression Dom_vital/e (Nc &NCc) containing the complex predicative (N & NC). This, as we shall see, is an essential dialectical term here characterizing the vital domain.

We must presume that our hypothetical animals are in the possession of some non-linguistic “notion” about–or at least some simple experience of–that temperature domain in which they can live. If such an experience shall be somehow “conscious” to the animal it must have “meaning” to it and so have achieved the character of a quale. Cotterill refers to different quasi-automatic reactions in primitive organisms like bacteria (using “random walk” behavior to come nearer to or farther away from “good” or “bad” sources) or like our hypothetical insects doing some “probe-by-movement” actions relative to their environments. In this connection Cotterill recognizes that at least higher organisms must further be in possession of such “notions” (based on his hypothetical “schemata”) so that these organisms also may realize what Cotterill calls “probe-by-proxied-movements”:

Even on the simpler “probe-by-movement” basis it will be possible for the animal to “warn” itself if it makes dangerous movements, thereby anticipating the threatening consequences (for instance, pain) of going too far in the direction of hot or cold. So we must presume the existence of such schemata concerning the essential conditions for performing safe behaviors relative also to the “notion” of temperature. So these schemata in the organisms react just like the switching mechanism of the thermostat.

To go one step further in direction of “intellectualization” we shall now, in contrast to simple “notions,” turn to the real behavioral process of temperature measurement. This demands, first, that we already have a well-established notion of temperature as such; secondly, that we also have material devices for estimating temperature beyond simple feelings (qualia); thus we strongly (historically) depend on the existence of readymade thermometers, and, finally, that we also linguistically and numerically are able to operate with these notions, that is, that we mentally have the necessary words and numbers at our disposal. So, now we take our thermometer and look at the column of quicksilver in the tube. See figure 3.

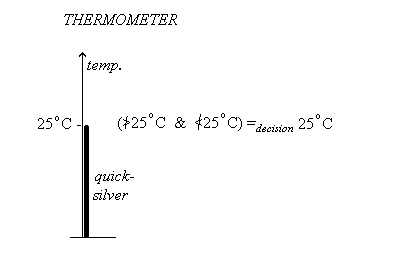
Figure 3

We observe (to the left) the quicksilver along the temperature scale reaches the mark 25° C. We now might be content with saying that the temperature of the room is 25° C. However, we could observe the device more carefully: Does it really point to the 25° C mark, or is it a little below, or possibly a little above? No! Under the given conditions of observation we must judge that the temperature is really neither below nor above 25°C. So now we state that the temperature is 25° C. But how can we say that? In our thoughts we have indeed imagined a couple of “probe-by-proxied-movements”–the “proxied“ movements just being “conscious” to us relative to our “notion” of temperature–the one seeking below, the other seeking above this mark. Obviously, no one of these probings gave defendable results; we have to deny these possibilities. Eventually we stop the measuring activities and simply (to the right of the figure)decide that the temperature is exactly (that is, unfalsifiably) 25° C. In our logical way of expression, therefore, we propose the following implication–on the basis of the subjective decision made under the actual observation conditions:

IF the temperature T /e (25° C &25° C), THEN T =_decision 25° C.

This implication as the “logical” result of a conscious “probe-by-proxied-movement” and the subsequent decision raises the primordial notion to the status of a genuine “concept” that formally has assumed the character of a “value” (here taking the form of a numerically expressed (measurable) parameter, but not necessarily) and as such generated by “abstraction.”

Using the above presented notation the sign > can reasonably be reinterpreted as C<, the crossing / meaning the simple negation N. So we write the following implication:

T /e ( N< 25° C & NC< 25° C) Þ _decision T = 25° C.

On this basis we judge T = 25° C to be true. But what does that mean for the concept of “truth” in general? It means that “truth” as such can in no way be something existent in the world. Quite on the contrary, generally it means that “truth” to the extent that it is itself a “value” is an ideal construction made under given material, subjective, and social (communicative) conditions.

4

This expression, indeed, at the same time offers us a genuine concept of identity. If by comparison (for example, relative to temperature) one thing (A) is neither smaller nor greater than another thing (B), and when < and > may be interpreted as any couple of moments, properties, characteristics, and so on standing in the mutual relation of contra-affirmation, that is, when > = C<, then the complex term (N< & NC<) as the predicative of the sentence B/e ( N<A & NC<A) is valid and the things A and B are–under the specified aspect–equivalent. This, in other words, means that their compared (measured) magnitudes in the sense of “values” (indicated by []) of the explicitly defined dimension are identical; we therefore write [A] = [B]. In this case the “values” can be numerically mediated (insofar as they are isomorphic to the rational number system) and consequently these “values” may be expressed by means of real numbers (their denominations assuming the dimension, or parameter, in question).

In this sense the concept of identity itself represents a “generative” valuation moment of the “intellectual” work to obtain “objective” knowledge about the thing in case. But even such a primordial moment of generativity must have been realized under certain social conditions to make people capable of this form of “intellectual” decision-making. This then, has, on the basis of the primordial “notions,” introduced once and for all a further constraint on consciousness, which hereafter “intellectually” expresses itself in binary terms (using the negation “not,” N, in its strong sense). Quite trivially, nevertheless, all of this simply means that two things in a certain sense either are valued as identical, or they are not. In other words, linguistically expressible identity must (unfalsifiably) be declared either “true” or “false”–thereby introducing the quasi-axiomatic assessment of the non-existence of any third possibility of thinking, tertium non datur.

This conscious activity of “probing-by-proxied-movement” and the following act of decision really anticipate a form of (only linguistically expressible) generative-dialectical logic. But how are we to “defend” such an “intellectual” activity and its actual emergence? In what context and under which conditions could such a way of thinking, the first time, have had any meaning at all? On the other hand, this question concerns nothing less than the concept of “Truth” as such. What does that mean? Even our hypothetical insects realized their simple form of behavioral adequateness, “rightness” and practical “truth”; but such “truths” cannot be linguistically mediated and explained like the numerical “truth” of the thermometer reading. Neither do they represent “Truth” as such, whatever meaning we might give the capital letter. We can only assume that inherent in “Truth” we find the dialectical contradiction of subjectivity and objectivity, the one side of this opposition inseparably connected to the other. Indeed, other forms of “truth” might be grounded in other domains of life, in religious belief, or simply in the everyday functionality of common human activities, all of them being subject to relevant decisions on the basis of likewise relevant “probe-by-proxied movements.” More or less logical reasoning in this sense, measurements, and so on, have been realized for millennia and purified in genuine scientific work–but seldom reflected on as intellectual creations in themselves.

b ) Parmenides’ “Way of Truth”

Thus the real question is how concepts such as “Truth,” “Identity,” and “Congruence” in particular could emerge at all. Common sense notions of “truth,” “correctness,” “rightness,” and so on are not identical to logical truth based on predication and proof. On the contrary, we should ask how “proofs” in general could be reduced to purely linguistic operations in the sense of Cotterillean “probings,” but under the strict condition of their linguistic mediation. This question is essential to understanding the specific Western way of thinking and its emergence.

In the history of philosophy the first remarkable example of this way of thinking is given by Parmenides and his famous concept of the “One.” In his great essay Prologue to Parmenides, Giorgio de Santillana asks with the words of John Burnet, which he calls “words of wisdom”:

De Santillana characterizes the introduction to Parmenides’ famous hexameter poem in this way:

This original Female principle of production and reproduction, the Goddess herself–de Santillana identifies her to be no less than Aphrodite Ourania, the “Daemon who steers all things”–unites two seemingly contrasting aspects, the intellectual and the physical, into one and the same universal principle of absolute, pre-Olympian power (cf. ibid., p. 88). Thereby de Santillana attempts to “look at the formal and mythical element” on the explicit basis of the new possibilities that Greek culture’s beginning literacy and social self-consciousness offer its thinkers. Hence the issue must be more than an explication of some personal notions. “Given the character of the poem, which is evidently an “intellectual purification,” and the straight Pythagorean lineage of the author, we might speak of a Hieros Logos, a Sacred Discourse” (Ibid, p. 85).

One problem about this “Sacred Discourse” is the meaning of the term doxa, “opinion without any pejorative connotations.” “It means, barring supernal knowledge, the kind of conclusions a man has been able to reach and is willing to stand by. . . In Pythagorean language, it is equivalent to “scientific inquiry” pure and simple” (ibid., p. 84). From quite another perspective, Wolfgang Lefèvre in his Rechensteine und Sprache (1981) mentions that this “science” to a great extent operated through material means such as reckoning-tokens, that is, exactly by means of materially realized and intellectually reflected-on specific “probings-by-proxied-movements.” However, Lefèvre also adds that the results of such operations were explicitly expressible only through language, this medium alone having the necessary strictness to be the genuine medium of unfalsifiable “truth.” We should remark that this form of scientific work uniting “the world of sense” and “the world of ideas” contains no hints of meaninglessness at all.

Parmenides’ “Way of Truth is,” as de Santillana says, “without any doubt, one of the most impressively obscure affirmations in the history of thought.” “But,” he adds, “if the way of Opinion is a physics–and it has taken centuries of exegetic blinkering to obscure this obvious fact–then the Way of Truth must make a sense which is correlative to that” (ibid., p. 89).

Essential is here that the Way of Truth ascertains indivisibility of Being, its inseparability, wholeness, continuity, permanence: “the idea of a homogeneous plenum seems to be passionately insisted on” (p. 90). So, “the substrate of all things is found back where it should be–everywhere, rather than nowhere” (ibid., p. 91). This he attempts to prove unfalsifiable.

De Santillana solves the problem of Parmenidean Being as follows:

This philosophy emerging about 480 B.C. was a clear and revolutionary breakthrough expressible only by a non-visualizing and therefore purely linguistic, abstract representation. So de Santillana concludes:

“Is this, then, the Truth?” de Santillana asks. Non-being–as a “Non-body-of-my-thought”–is non-thinkable, “is not to be spoken of.” The answer, therefore, must be Yes. But we have no organ “that can be imagined as grasping Being.” “This is indeed the first time in which thinking has to mean “being aware” in an explicitly different sense than that of perceiving or imagining through phantasia.” (Ibid.) And this “being aware” in the course of time and under new conditions just developed into the modern measuring sciences.

6

Exactly this idea of the abstract “space” in the sense of a “homogeneous plenum”–if de Santillana is right in this interpretation of Parmenides–realizes the concern of all theoretical sciences: to find the substrate of things, the One that unifies the Many, the Pythagorean numbers or the Euclidean points having positions, relations to each other, and so defining the homogenous geometric background for all that happens in reality. The non-limit as bearer of position and number itself carries in it the very determination of position and other forms of the limit. As mentioned above, for example, the concept of “parameters” represents just such a “non-limit.” Any logical concern with such ideas brings forth the idea of the homogeneous continuum underlying it, some kind of “substances”–eventually even bringing forth the idea of the “irrational,” the “existence” of which, nevertheless, is “not to be spoken of”–at least until new forms of awareness of concepts have been generated (cf. ibid, p. 102).

So, on this complex background, outside geometry “mathematical theory” cannot be anything but a general numerical theory of magnitudes, of “values” in this sense, representing exactly such specified abstracta and “homogenous plena” based on the equally abstract concept of congruence and identity.

We really have to acknowledge this Parmenidean breakthrough of about 480 B.C. in a revolutionary way, as generating these non-material, therefore merely linguistically (possibly numerically) expressible abstracta, just what Hegel described as Begriffe, or–in the terms of Cotterill–the development from more or less diffuse qualia-based notions to exactly defined logical concepts produced under the condition of “probing-by-proxied-movements” on the basis of literalized language.

However, an essential moment not to be forgotten in this connection is the mentioned postulate of the participation of the Goddess herself, Aphrodite Ourania. Why this divine ingredient in this conceptual generation? Her ideal existence, certainly, must be grounded on contemporary mythic-religious rites (especially in the secret religious “lodges” of Elea and the Pythagoreans). Consequently we must ask how there could emerge the mode of abstract conceptual thinking that Hegel had in mind. Our attempt to answer this question will lead us into further domains of generative dialectics.

c) Rappaport and “The Obvious Aspects of Ritual”

To take this further step we shall refer to the essay “The Obvious Aspects of Ritual” by Roy A. Rappaport, reprinted in his book Ecology, Meaning, and Religion (1979). If we accept that Parmenides’ ritualistic background cannot be quite contingent but must have some relevance to the development of his “Way of Truth” then we must take notice also of this profound analysis of the meaning of ritual and liturgy in general.

Like Hegel, de Santillana saw the Parmenidean “Way of Truth” as the “transition from the stage of Vorstellung to the stage of Begriff” and called the overture to the Parmenides’ poem “a grandiose and mythical adventure” led by the great Goddess Aphrodite Ourania. So Parmenides’ journey behind the “Pillars of Day and Night” must itself be characterized as a grandiose generative event, even an epochal one in terms of philosophy. Below we shall again compare this “generative event” to other simpler, “objective” measurement events (and to equalization and comparison events in general, for example, payments on commodity markets), thereby defining their mutual analogy.

We shall therefore suppose that Rappaport’s essay too defines a “generative event,” being a study of religious experiences essential to all mankind in the form of rituals, and we shall attempt on this basis to give a formal definition of such an event. Our purpose is not to declare all such “events” to be similar, nor to affirm the necessity of religious experiences in philosophical and scientific work, but rather to reveal the similarity of their forms and dialectical structures that establishes them as analogous. In short, we shall show each of these forms to be representative of the same general form of “generative event,” the key structure of generative dialectics.

Rappaport distinguishes between two double-negative concepts, one defined as the unfalsifiable, the other as the undeniable. He relates unfalsifiability to the “sacral” aspect of ritual and the concept of the “numinous”–thereby referring to Rudolph Otto (1926)–to ritual’s undeniable aspect. Finally he defines ritual as such as the unification of these–in themselves contradictory–conceptual structures. In the traditional manner of dialectic, we recognize these aspects to be distinguishable but inseparable.

In the sense of logic we must here distinguish between “outer” negations of a statement (sentence) in the sense of denial (traditionally indicated by the sign Ø: “It is not true that…”) and “inner” negations of the predicate in the sense of “not” (indicated by the sign ~). It will then be possible to give a quite formal–or, as Rappaport calls it himself, a “meta-logical”–definition, first, of these two aspects of ritual singly and, finally, of ritual as one behavioral whole.

7

To achieve this, let us try to interpret these expressions in words and then by means of logical signs to give these dialectical concepts their formal definitions. We shall use the signs ¦ for false; w for “true” (= not-false); finally, we introduce the terms s for the simple ostensive form of expression and m for the manifest ostensive form of expression to indicate that to the minds of the participants themselves these religious experiences indubitably emerge out of the ritual situation as such. We then obtain the following definitions (where !, opposite to Ø, means “It is true that…”):

The Sacred (unfalsifiable): This manifest ostensive is declared in principle non-false: !m/e ~ ¦ (= /e w). [It is true that m is not-false (= is true)]

It is of interest here that Rappaport relates the “numinous” in the sense of the undeniable to forms of anthropogenetic evolution, thereby viewing language as a specific moment emerging from the very process of ritualization to be found, indeed, even among animals–this being also a central theme of GA, the introduction of the sign to establish the acculturation of anthropoid groups. On the other hand, behaviorally these domains of falsity and non-falsity can be controlled by “probe-by-proxied-movement” tactics in the sense of Cotterill, and thereby in the given social context threaten ritual-breaking participants with excommunication or other difficulties. On this basis human ritualizations may easily have developed out of forms of animal ritualization, generating the stable ethological background necessary for symbolization (e.g., language) to emerge. Hence ritualization might be the necessary generative moment not referred to by de Santillana. The crucial moment here is that any confirmed form of falsifiability as such (as well as its opposite, unfalsifiability) must be viewed precisely as the consequence of ritualization in general and the creation of language in particular. So the negation marker “not” of the primary formulae could directly refer to some breaking out of that ritual “invariance,” indicating a kind of “more” or “less” (“hybris”) or simply refer to the general ability of developed language (possessing the declarative sentence) to combine words more freely than ritual had originally prescribed.

Formally, therefore, the evolution undeniability ® unfalsifiability may be expressed by the transition: Ø s/e ¦ ® !m/e ~ ¦ » – but notice that this last term seemingly involves comparison, decision, etc. That is, on the basis of the undeniability of the simple ostensive “impossibility of stating something false” (cf. Parmenides!) there follows (temporally, logically) the certainty of the corresponding manifest ostensive (predication, judgment) emerging under ritual conditions as unfalsifiable. This would in common language mean that such social predications–here in the sense of the ritually defined sacred–are always true, that is, representing the social “Truth.” However, this “Truth” must concern the whole ritual situation, including its sacred utterances and their meaning, taken as an originary form of the manifest ostensive; this truth is opposed to that of the declarative, truth in the sense of the rightness of individual linguistic or numerical propositions. In our connection here, however, the negative term “un-false” is of quite special interest. In the light of the discussion above about the decision made in reading the measurement device, this means precisely that we cannot make such singularized truths “sure” in any other way than–under the given conditions–by deciding them to be so, that is, just un-false, respectively by “believing” in their non-falsity as expressed by the complex predicativeof the neither-more-nor-less (N> & NC>).

However, a severe problem is veiled in this formal expression. On the one hand, the predicative presupposes as mentioned above predicative expressions the truth-value of which must be either decided or simply “inherited” through correct logical deduction. This must be considered an unsound condition. On the other hand, the predicativein the sense of the neither-more-nor-less (N> & NC>) also presupposes a conscious decision-making in a concrete situation of intellectual “navigation” among different questions at issue. This cannot be a valid model for understanding rites more often experienced as behavioral wholes rather than singular examinations of the environment.

These objections might be related to Parmenides’ abstraction of space (according to de Santillana) defined as the comprehensive One, the homogeneous plenum containing nothing but relations, “all-the-relations-there-is.” This, indeed, must be the very foundation of geometry in the form in which we have inherited it from the Greeks–but only its “foundation.” This apprehension of “space” is the condition for all subsequent geometrical knowledge and single geometrical “laws” formulated, for example, in Euclid’s Elements. These Euclidean “truths” must necessarily be seen on the background of the “Truth” of Parmenides.

8

On the basis of Rappaport’s essay these formal considerations can be related to de Santillana’s discussion of Parmenides. First Rappaport states, concerning the principal concepts of the sacred, the numinous and ritual as such:

Rappaport’s essay contains other remarks of great interest in connection with this last comment. If in the light of the Parmenidean “Way of Truth” we consider the analysis of the discursive sacred in relation to our previous analysis of the temperature measurement process, taken as our general model of measurement praxis, then, indeed, we find also on this point astonishing parallels. Rappaport writes:

I would hesitantly suggest that the notion of the divine has at least four features. First, while divine objects may be incarnated, the quantity of the divine itself is not material in any ordinary sense. Second, the divine exists, or, rather, has being. It is not deemed to be, simply, a law, like the laws of thermodynamics, or an abstraction, like truth, but a being, like Zeus. Third, it is powerful, or efficacious. It has the ability to cause effects. Finally, it is something like alive. It possesses something like vitality. To use Rudolph Otto’s term, it is “urgent.” (Rappaport 1979, p. 215)

What Rappaport here “hesitantly” suggests is certainly, on the one hand, in most beautiful accord with our measurement analysis. The aim of measurement is to determine “values,” here the value of a given temperature; but we have assumed that a “value,” too, may have different forms depending on the conceptualization that generated it, that is, abstracted it as “value.” All this will be even more striking if we interpret “values” in the more specific sense of economic values of commodities being “measured” by purchase on the market. Just in this form “measurements” are certainly most essential to the whole way of material life in society today and so also most relevant material for “probing-by-proxied-movements.” Consequently, in a society built on an universal interest in manipulating physical, economic, and other abstracta, here called “values,” these values and their material carrier-bodies will be just such “mystical” (cf. Marx: “fetishist”) “divine objects,” generally endowed with specific social meanings.

In this last quotation about this “divine object,” Rappaport even challenges the Pauline opposition between the “Christ” kata sarka (i.e., “Christ according to the flesh”) and the “new,” mystical nature of Christ in his own teachings. Incarnation here means an implicit acceptation of the “monophysite” view of Christ and of humans in general. In this connection we even notice that this “sacred” value is quantitatively incarnated, that is, the “sacred” as such indicates or itself “contains” a certain quantity of this divine moment, even if this “is not material in any ordinary sense.” Hence, secondly, such values “exist,” they “have being” and this even in a powerful way. The final point by Rappaport could perhaps be more difficult to assess. But if, following Karl Marx and others, we accept specific economic and socially essential “value” as the product of productive human labor, that is, of a form of the very human vitality over time, then we really, like Otto, might call this determining moment of the market economy “urgent”–although not necessarily associated with Zeus himself or other Gods or Goddesses.

9

Although the concept of “value”/”the sacred” would be unthinkable without language, it seems common sense to suggest, first, that possibly language and the social order founded on language could not have emerged without any support of the numinous, nor possibly numbers without reference to socially interesting magnitudes and other values of some kind–and, secondly, that natural sciences could not have emerged at all without mathematical support and implicit knowledge about “space” as such. Exactly counting and measuring are the intentional processes in which material things are ideally reduced, or converted, into abstractions, to mere idealized carriers of “values.”

However, a most essential problem of language as well as of magnitudes is that both may lie. Therefore, the general need for socially accepted, confirmed, invariance of religious liturgy as well as the equally confirmed invariance of scientific praxis and the terms used to generate real truth; such generation, or “production,” must follow the most generally accepted sacred laws of identity and, correspondingly, a generally accepted (“sacred”!) methodical (“meta-scientific”) “law” of scientific work as such. However, this again actualizes the opposition mentioned above between the “logical” (= true) prepositions and the “meta-logical” conceptualization of the One; between the true Euclidean sentences and the Truth of the Parmenidean “space” as the homogenous plenum; between “scientific” work and the fundamental, more philosophical, “meta-scientific” forms of work. All of these “meta-“terms contain moments that must necessarily be implicitly accepted as fundamental to the very ways of thinking and arguing–presumably contained simply in the specific syntaxes of the languages or formula systems used–and hence endows the concepts in question with the necessary unquestionable, just undeniable evidence (an immediately felt truth) under the given social/historical conditions. This unquestionable evidence transcends in a fundamental way all questions about more specific qualitative and quantitative congruencies and identities, the “neither-being-more-nor-less” and so prepares for the sacral “Word,” the “Logos” (cf. St. John 1.1), and the very “Truth.”

Rappaport himself expresses this idea as follows:

Let us follow up the above discussion by recurring briefly to our initial definition of measurement. On the basis of the distinction between the different forms of negation we now shall introduce the new sign <x|y> to characterize the fundamental function of anticipation; <x| indicates an acknowledged initial situation in which an actualized future state or event |y> is anticipated. So y necessarily has to be defined as the positive (necessary, not accidental) negation (the contra-affirmation, C) of x, y= Cx. If this was not the case it would have been impossible to experience any form of causal, logical or other form of entailment between events. Without the function of anticipation all change would be nothing but inexplicable “random walk.” No “meanings” would be found at all. But this also means that anticipation as a temporary intentional function introduces time and hence an essential moment of generativity as defined above; through anticipation we “construct” in a self-referentially “meaningful” way what we are “seeing” as being just “our” experience. So, anticipation also defines the very moment of creativity in humans and other living organisms that anticipate aspects of the future, even in the more abstract sense of deducing unfalsifiable conclusions from logical (predicative) judgments. On this general basis we shall attempt the unification of Rappaport’s double definition into one single formal schema taking our starting point in

10

defining the results of the measuring operation by means of double negation in the sense of the generative dialectics:

“undeniability”	®	“unfalsifiability”
Ø s/e ¦	®	!m/e ~ ¦ »
experience	®	predicative declaration
observation	®	decided identity
It would be false to declare the temperature 25° C to be false; i.e., it cannot be false to accept the temperature measure 25° C.	®	After intense observation I decide that neither25° C nor 25° C is the case; i.e., I declare “not being false” to mean the “truth” of declaring the measured temperature to be = 25° C on the basis of the concept of “identity” defined by the predicative.

The transition from observation to decision using the terms of the simple (s) and manifest (m) ostensives we may define thus (where “manifest” means a historically developed contra-affirmatively defined form of operativity):

m » Cs ; or: !m/e w = CØ s/e ¦ = !Cs/e w.

Finally, this transition defines itself an anticipatory process analogous to the generative ritual process in which the “sacred” itself is anticipatorily defined as actualized on the basis of a realized (experienced) “numinous” moment. That is, we may also define the sacred (s) as the contra-affirmation of the numinous (n). So we get the

definition of the ritual situation as a whole through the socially conditioned anticipation

<Ø s|!m> » <~ ¦ | >, or <(s)|(n)>.

The same mode of argument was used above to define the real, so to speak, “scientific” (as well as economic, etc.) measurement of magnitudes (parameter values) in contrast to the simple everyday reading of thermometers (prices, etc.). The formal analogy between such everyday operations, Parmenides’ finding the very “Way of Truth” and Rappaport’s logic of rituals, the “numinous” and the “sacred” is remarkable. These three generative processes form a kind of evolutionary stepladder, the first step of which is clearly embedded in the animal world, the second in the religious world, and the third in the logical (predicative) world that emerged in Antiquity, the–until now–uppermost step leading up to the modern (mathematical and other) sciences. The defining term connecting these intentional domains is the same, exactly that of the generative (literal) dialectics.

e) Final comments

At this point we may ask how this theory of cultural genesis relates to Eric Gans’s Generative Anthropology (GA), with its hypothetical “originary scene of representation.” This “scene” with its “abortive sign” was proposed as the generative event preparing for the development of language and the function of symbolization and so for human culture in general. It has been objected to GA that this “scene” is too appropriatively defined and therefore fails to reflect to a sufficient degree the more general “social intelligence” based on complex inter-individual relationships in the groups of apes and other higher mammals now living. Hence the question must be whether the theory of GA including its critique can be reflected within the framework of the dialectical theory proposed here, primarily on the basis of Rappaport’s essay.

However, in the light of the theories of de Santillana and Rappaport there is, perhaps, no longer any real contradiction at all. Imagine again Gans’s hypothetical group of anthropoids, everyone equipped with dangerous canines and collected around a large beast of prey, all of them strongly obsessed with getting a big piece of the flesh for himself. As so often in the animal kingdom these “socially intelligent” pre-humans had learned some way of ritualizing their aggressive behavior into more peace-securing modes in order to prevent a disastrous fight of all-against-all. Presumably we must seek the solution of the anthropogenetic problem in the very transition from the non-verbal to the verbal form of group life (society) that Rappaport suggested to be an essential aspect of the transition from the “numinous” to the inclusion of “sacred” aspects of ritual. However, we may possibly have to assume the “numinous” to be just as dependent on its “sacred” contra-affirmation as the latter is on the “numinous” itself. This we attempted to formalize above as the anticipation defined <Ø s| !m> » <~ ¦ | >, where indeedwas characterized as the discursively “decided truth.”

11

But this interpretation needs further comment. Presumably, as just suggested, the “numinous” as such will not be experienced by any animal, as opposed to feelings of panic in a situation of crisis. Of course, we cannot know, but I think we have to assume this as a matter of fact, even as a precondition for all further arguments. Consequently we must assume that no animal ritualization immediately leads to proper “rituals” and “liturgies” in the human sense. Hence we have to revise the merely analytic formalisms above based on Rappaport. What formal relationship between “aggressive behavior” and the “ritualized behavior” of the hypothetical hominids has to be acknowledged here? Is it the relationship of (analytic) negation N, simply stating “ritualized behavior” to be non-aggressive behavior? I don’t think so. Even “ritualized behavior” is certainly aggressive, however positively transformed. We defined this form of negation as the contra-affirmation C. Calling “aggressive behavior” p we therefore shall call “ritualized behavior” a “no-longer” aggressive (rather than a non-aggressive) behavior, Cp.

At the opposite pole from Rappaport’s contrastive definition we find the “sacred” analogized to the identity-based logical judgments of, for example, Parmenides, leading to the logical and quantitative “modern sciences.” This point too, however, requires a critique. We have analogized this “identity,” homogenous abstract spatiality, to the constancy, permanence, and so on of all ritual behavior as basic to the notion of “eternity.” Now, on the one hand, as always we have in the case of anticipation to define the right actualized side of the opposition |y> as the contra-affirmation of the left confirmed one <x| . If we call this logical, identity-based, quantitative scientific qfrom the anticipation formula <p|q> we must here also write q = Cp; however, the “sacred” q cannot be the simple contra-affirmation of the primordial p (as the temporal “no-longer” p) but must rather represent its double-contra-affirmation CCp, that is, represent the contra-affirmation of the primordial q, that is, be Cq. In this sense, therefore, “sacred eternity” (as a temporal “not-yet q”) contra-affirms the modern concept of substantial or temporal identity. In the same sense p is contra-affirmed asCp but here too when q = Cp we nevertheless must say that Cp ¹ q. We notice the important distinction to be maintained between the (symmetrical) logical and the dialectical negations N and C.

Together these arguments oblige us to reinterpret the genuine “rituals” and “liturgies” formally by defining then by the predicative (Cp & Cq) where q = Cp. In an anticipatory formalization, therefore, in the sense of “no longer & not yet,” genuine ritual must be redefined exactly in the generative dialectical form as a “portal” opening onto new and immediately undecidable developments, of which the genesis of language (and other forms of symbolization as well as all the different “cultures” in general), later logic, market exchange, valuation and measurement, etc. are some of the more essential ones.

And exactly this term (Cp & Cq) also characterized the domain of life when seen from the vantage point of our speechless hypothetical insects (cf. figure 2 above). From this “portal” of undecidedness too new and unpredictable life forms sprout.

But we should also notice the remarkable formal similarity between the “Word,” the “One,” and even the hypothetical (abortive) “Sign” of GA–all of them just being negatively defined: without syntax, without (theological, geometrical, or other) sentence generation, and so on. Or, more positively (contra-affirmatively) and promisingly expressed, all of these “pre-concepts” represent forms of plena characterized by the term of the “not-yet,” being “not-yet”-syntactical, therefore making theological, geometrical, or other sentences “not-yet”-possible (“not-yet” Euclidean geometry, Galilean/Newtonian physics and mechanics, political economy, etc.)–but, on the other hand, “no-longer” animal (in earlier times therefore presumed “unconscious”!). And, finally, all of these comprehensive “pre-concepts” are generated in (real, presupposed, or hypothetical) extreme emotional situations–the importance of which is later intellectually, even very passionately(!) negated.

So we note the essential difference between the language-specific dialectical formulas

(Np & Nq) Þ Identity

and the generative dialectical one, the “portal”

(Cp & Cq) Þ ?!

Literature

Rodney Cotterill (1998): Enchanted Looms. Conscious Networks in Brains and Computers. Cambridge University Press.

Wolfgang Lefèvre (1981): “Rechensteine und Sprache. Zur Begründung der wissenschaftlichen Mathematik durch die Pythagoreer.” In: Peter Damerow und Wolfgang Lefèvre (Eds.): Rechenstein, Experiment, Sprache. Historische Fallstudien zur Entstehung der exakten Wissenschaften. Klett-Cotta.

Roy A. Rappaport (1979): “The Obvious Aspects of Ritual.” In: Ecology, Meaning, and Religion. North Atlantic Books, Richmond, California.

Giorgio de Santillana (1968): “Prologue to Parmenides.” In: Reflections on Men and Ideas. First M.I.T. Press Paperback Edition, 1970.